1 RUSLE model protocol

1.1 Introduction

1.1.1 Purpose

This RUSLE model is generated to produce a soil erosion map for our study area of the B07 project (based on the EHAS survey). This soil erosion map will later be used for a conditioned Latin hypercube sampling (cLHS) to choose sample locations. It was based on the originals equations from Renard et al. (1991).

1.1.2 Procedure

We follow Thapa (2020) procedure for the RUSLE model based on 5 factors: rainfall, soil strength, slope, land use and conservation. We also used Cossart, Fressard, and Chaize (2020); Almagro et al. (2019) and Mehri et al. (2024) as reference work. The DEM has been filled with the SAGA GIS function Fill Sinks (Wank & Liu); SAGA GIS 7.8.2 version.

Methodological framework for potential erosion using RUSLE model (from Thapa, 2020).

Figure 1.1: Methodological framework for potential erosion using RUSLE model (from Thapa, 2020).

1.1.3 Input data

All the data listed below are available freely online.

(#tab:imput_1)Data used in the production of the RUSLE model.
Name/ID Original resolution (m) Type/Unit Source
DEM/TE.5 25 Meters ESA and Airbus (2022)
Prec. sum/OT.6 1000 mm WorldClim2 Fick and Hijmans (2017)
Landuse/OT.4 10 - Zanaga et al. (2021)
WRB Soils/OT.11 1000 - HWSD v2.0 FAO and IIASA (2023)

1.2 Equations

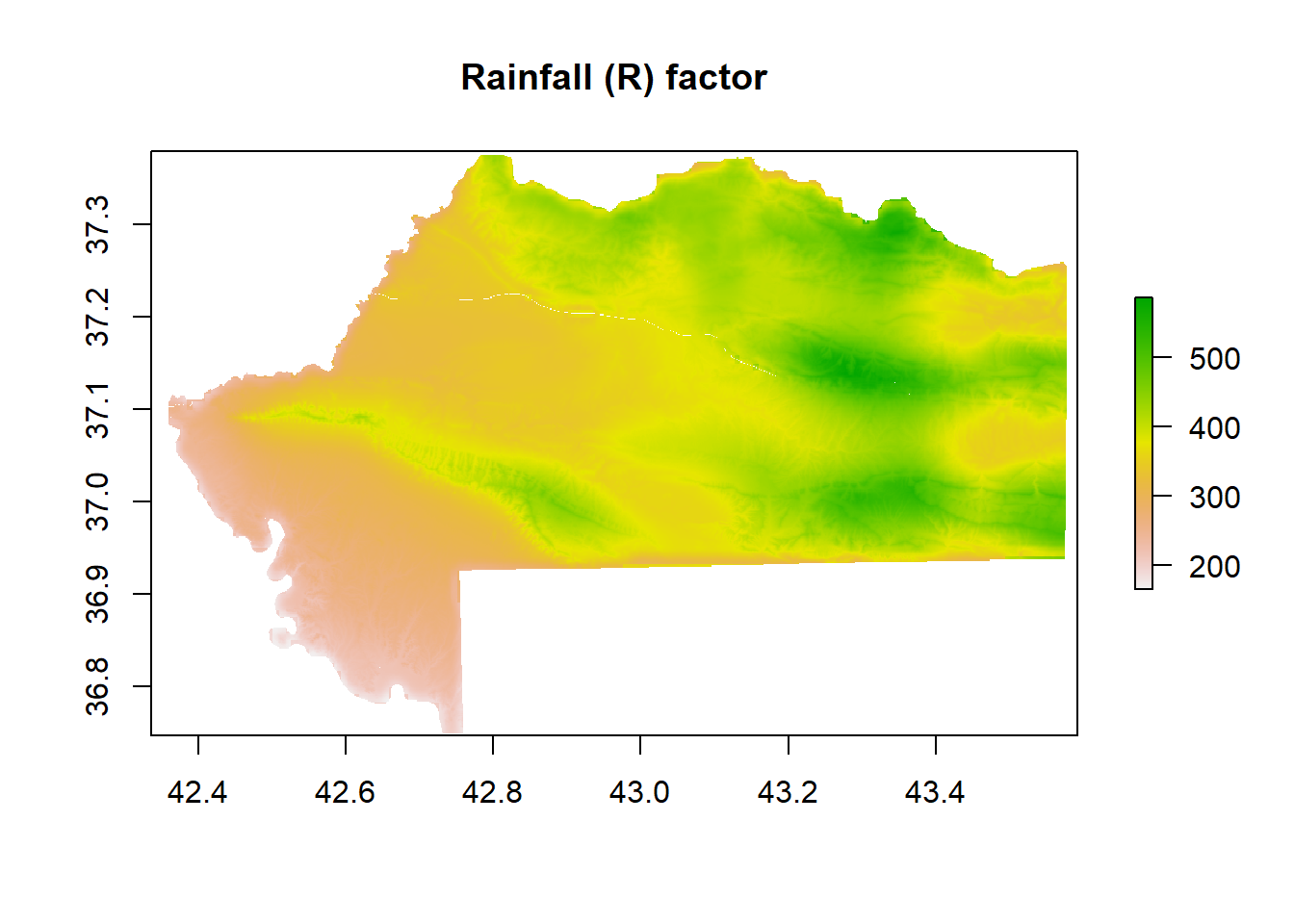
1.2.1 R Factor

It is the precipitation factor computed from the precipitation raster based on Morgan et al. Morgan, Morgan, and Finney (1984):

\[ R = 38.5 + 0.35P \] For P = precipitation per year in mm.

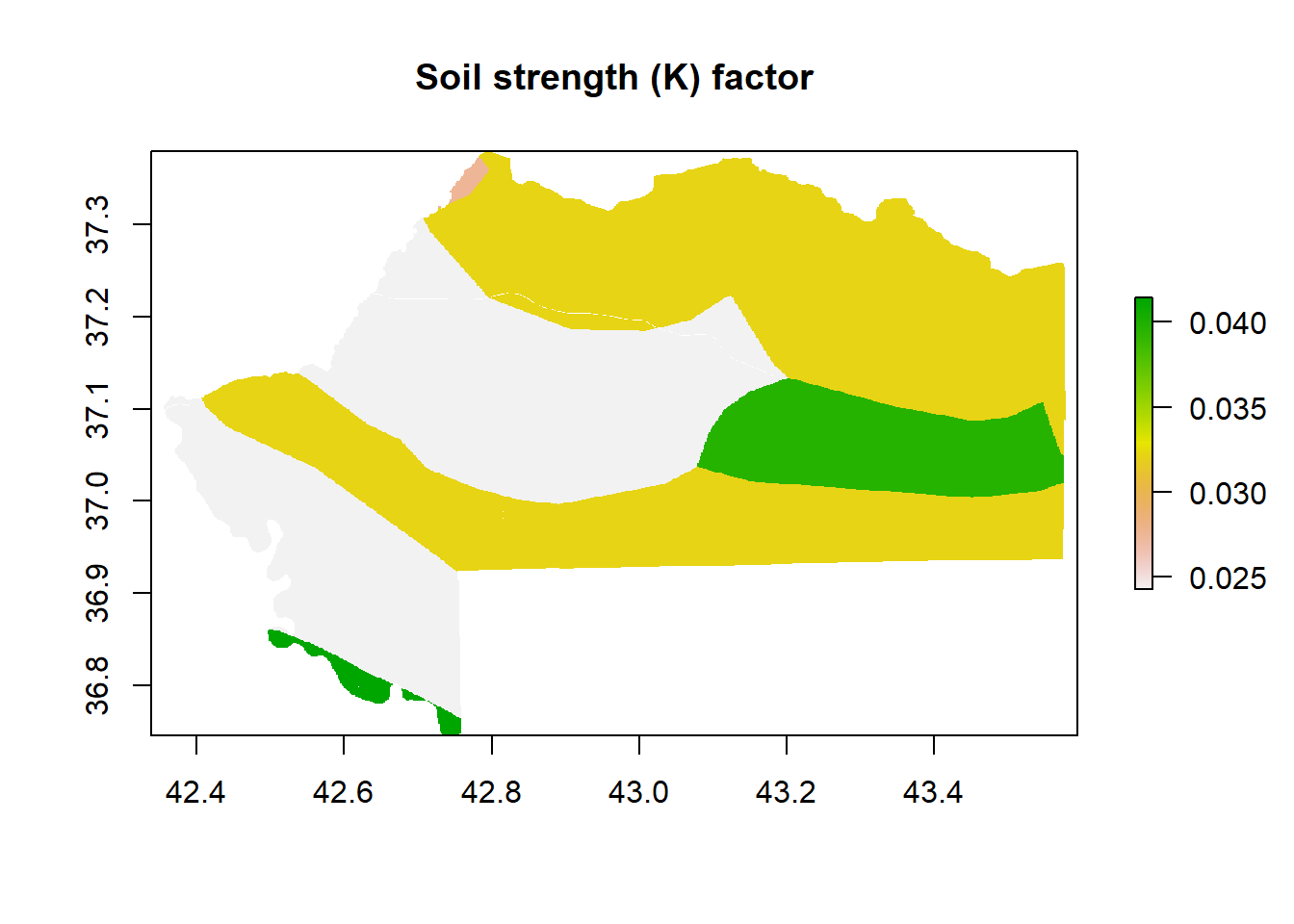
1.2.2 K Factor

Is the soil strength factor computed from different parameters from soil map based on Kouli et al. Kouli, Soupios, and Vallianatos (2009):

  • SAN = Sand in %
  • SIL = Silt in %
  • CLA = Clay in %
  • C = Soil organic carbon in %

\[ Fcsand = 0.2 + 0.3exp(-0.0256 SAN(1 - \frac{SIL}{100})) \] \[\\[0.5cm]\] \[ Fsi-cl = \frac{SIL}{CLA+SIL}^{0.3} \] \[\\[0.5cm]\] \[ Forgc = 1- \frac{0.25C}{C + exp(3.72 -2.95C)} \] \[\\[0.5cm]\] \[ Fhisand = 1- \frac{0.7(\frac{SAND - 1}{100})}{(\frac{SAND - 1}{100}) + exp (-5.51+22.9 (\frac{SAN - 1}{100}))} \] \[\\[0.5cm]\] \[ K = Fcsand * Fsi-cl *Forgc *Fhisand *0.1317 \]

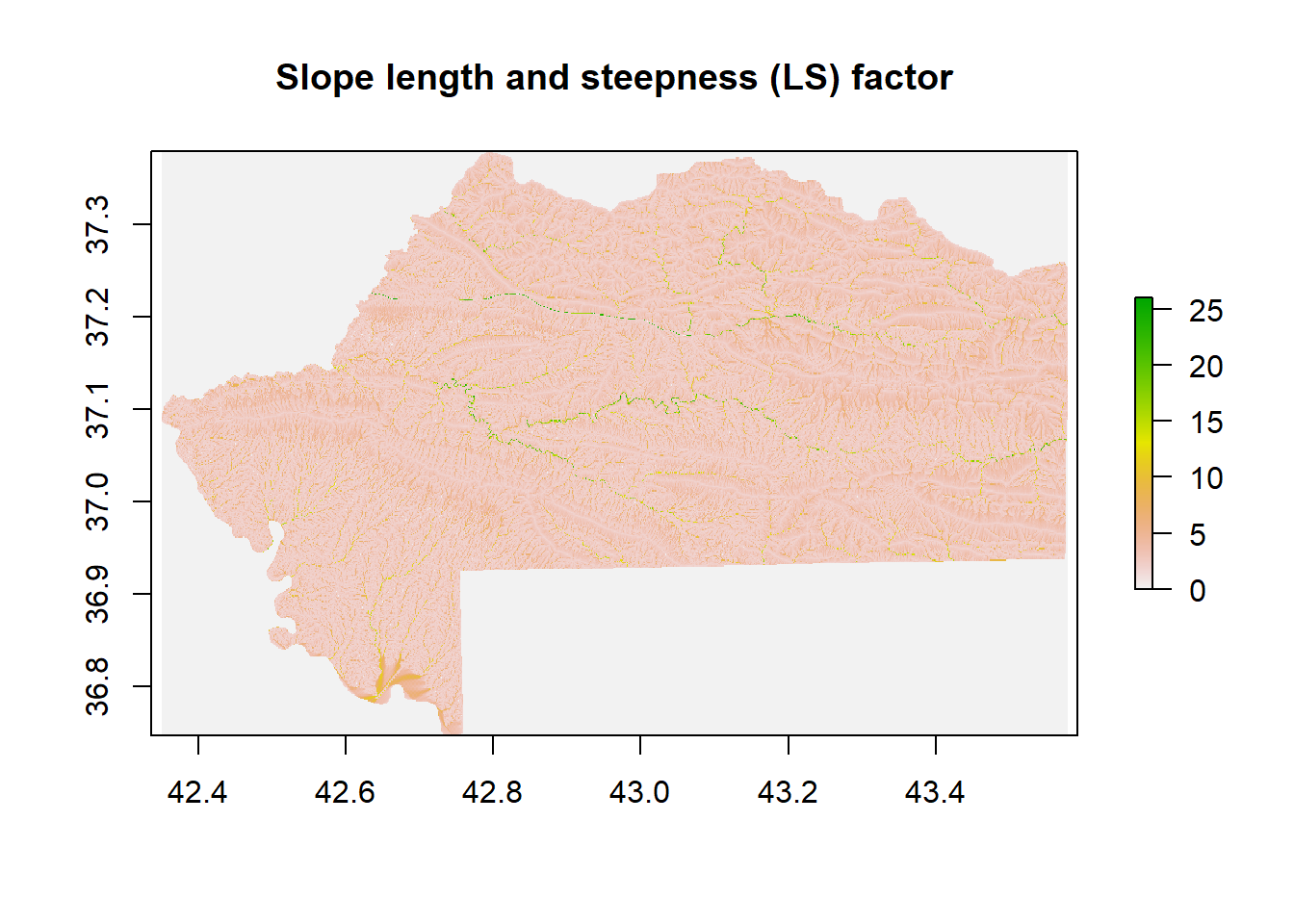
1.2.3 LS factor

The slope length and steepness factor was computed from the DEM under SAGA GIS 7.8.2. We used the LSFactor single way with the Desmet and Govers 1996 method.

SAGA Ls factor with the One Step tool.

Figure 1.2: SAGA Ls factor with the One Step tool.

For more detail of the LS parameters:

  • \(S_j\) = Slope factor for the j-th segment.
  • \(\lambda_j\) = Distance from the lower boundary of the j-th segment to the upslope (m).
  • \(m\) = length exponent of the RUSLE Ls factor.

\[ LSj = \frac{Sj(\lambda_j~^{m+1}-\lambda\frac{m + 1}{j - 1})}{(\lambda_j-\lambda_{j-1})22.13^m} \]

1.2.4 C factor

It was based on the land cover map of Copernicus data set and divided into 6 different classes. Then, based on a literature review, a ratio was established (Morgan 2005; Swarnkar et al. 2018).

Table 1.1: Ratio of C factor between different land uses.
Land use Value
Water 0
Forest 0.001
Shrubland 0.01
Urban Area 0.1
Cropland 0.2
Wasteland 1

1.2.5 P factor

P is the conservation factor value. It is difficult to establish in the region as no previous work has been done. As no value was known for this factor, we put a 1 value default as in Mehri et al. (2024).

1.3 Results

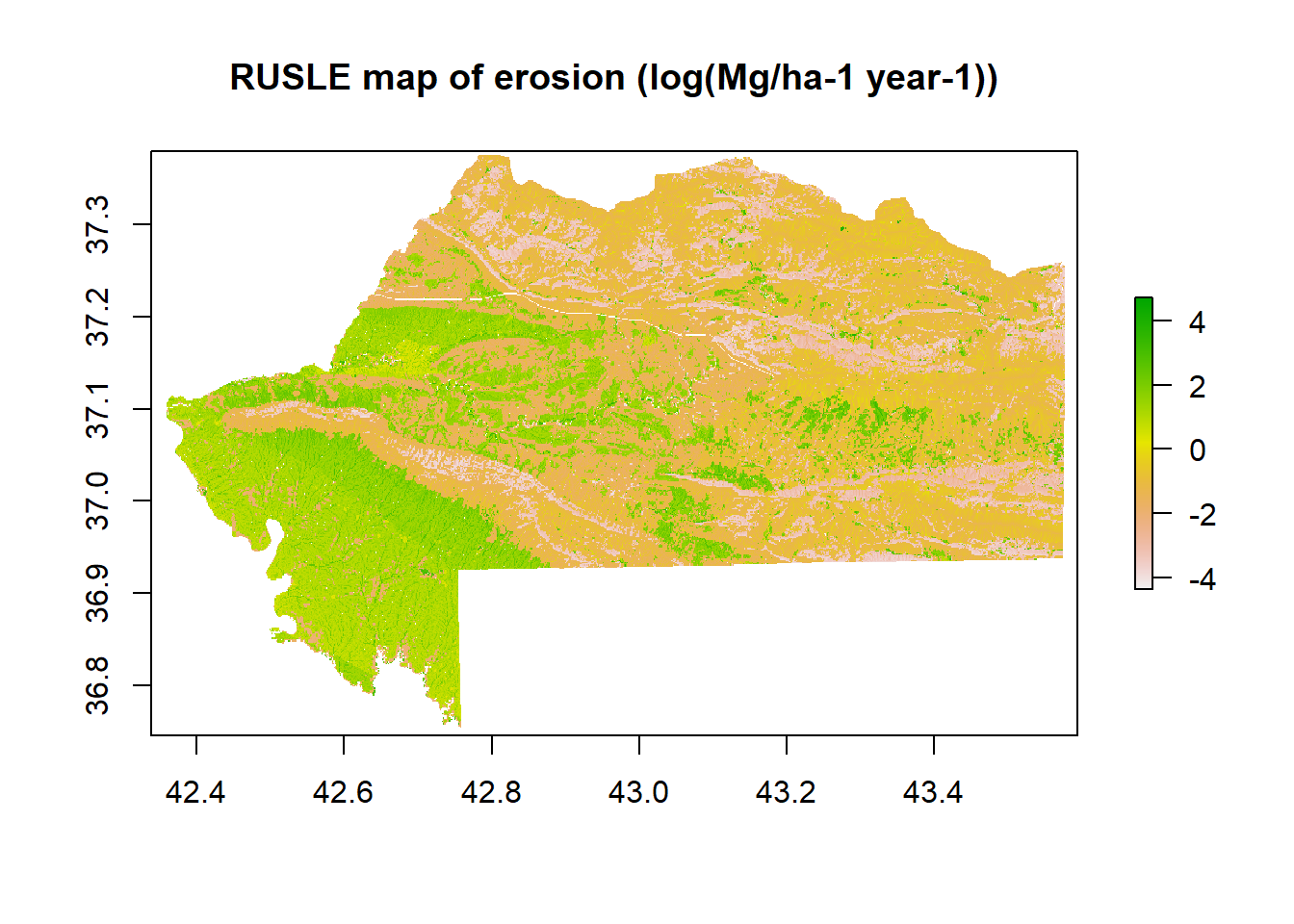
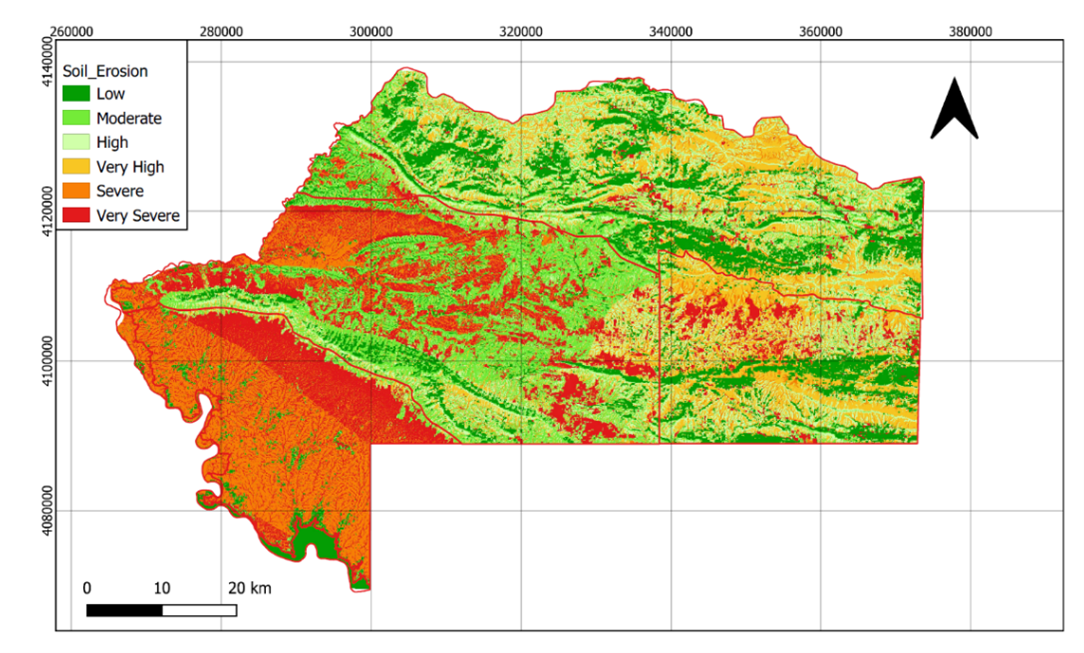
The erosion map shows a low erosion at Mg/ha-1 year-1 in terms of quantity. Most of the values are under 1.7, and only a few are above it. However, with a quantile classification (not based on continuous classification), we were able to spot the area with more erosion. It is mainly an area on the south of the Be’khair anticline in the Swaka Tika anticline and the upper region of Zakho (under the anticline). The northern and western areas are more preserved from soil erosion as the high anticline is probably due to less land use and forest presence. When the slope factor mainly influences the wadi and river border, the precipitation factor strongly influences the upper Khabur valley. The soil factor seems to have a minor influence on the middle and upper Khabur valley and on the right bank of the Tigris. The most preserved areas are the river and Mosul Lake.

Table 1.2: Basic statistics for the erosion map based on RUSLE model.
Statistic Value (Mg/ha-1 year-1)
Min. value 0
Max. value 117
Mean value 1.17561
SD 3.1574

1.4 Annexes

RUSLE map of erosion with breaks calculated by quantiles (WGS84, UTM38N).

(#fig:erosion map gradient)RUSLE map of erosion with breaks calculated by quantiles (WGS84, UTM38N).

References

Almagro, André, Thais Caregnatto Thomé, Carina Barbosa Colman, Rodrigo Bahia Pereira, José Marcato Junior, Dulce Buchala Bicca Rodrigues, and Paulo Tarso Sanches Oliveira. 2019. “Improving Cover and Management Factor (C-Factor) Estimation Using Remote Sensing Approaches for Tropical Regions.” International Soil and Water Conservation Research 7 (4): 325–34. https://doi.org/10.1016/j.iswcr.2019.08.005.
Cossart, Etienne, Mathieu Fressard, and Brian Chaize. 2020. “Spatial Patterns of Vineyard Landscape Evolution and Their Impacts on Erosion Susceptibility: RUSLE Simulation Applied in Mercurey (Burgundy, France) Since the Mid-20th Century.” ERDKUNDE 74 (4): 281–300. https://doi.org/10.3112/erdkunde.2020.04.04.
ESA, and Airbus. 2022. “Copernicus DEM.” https://doi.org/10.5270/ESA-c5d3d65.
FAO, and IIASA. 2023. Harmonized World Soil Database Version 2.0. FAO; International Institute for Applied Systems Analysis (IIASA); https://doi.org/10.4060/cc3823en.
Fick, Stephen E., and Robert J. Hijmans. 2017. “WorldClim 2: New 1‐km Spatial Resolution Climate Surfaces for Global Land Areas.” International Journal of Climatology 37 (12): 4302–15. https://doi.org/10.1002/joc.5086.
Kouli, Maria, Pantelis Soupios, and Filippos Vallianatos. 2009. “Soil Erosion Prediction Using the Revised Universal Soil Loss Equation (RUSLE) in a GIS Framework, Chania, Northwestern Crete, Greece.” Environmental Geology 57 (3): 483–97. https://doi.org/10.1007/s00254-008-1318-9.
Mehri, Azade, Hazhir Karimi, Yaseen T. Mustafa, Ayad M. Fadhil Al-Quraishi, and Saman Galalizadeh. 2024. “Predicting Soil Erosion Using RUSLE Model in Duhok Governorate, Kurdistan Region of Iraq.” In Earth and Environmental Sciences Library, 171–87. Cham: Springer International Publishing. https://doi.org/10.1007/978-3-031-58315-5_9.
Morgan, R. P. C. 2005. Soil Erosion and Conservation. 3rd ed. Malden, MA: Blackwell Pub.
Morgan, R. P. C., D. D. V. Morgan, and H. J. Finney. 1984. “A Predictive Model for the Assessment of Soil Erosion Risk.” Journal of Agricultural Engineering Research 30 (January): 245–53. https://doi.org/10.1016/S0021-8634(84)80025-6.
Renard, Kenneth G., George R. Foster, Glenn A. Weesies, and Jeffrey P. Porter. 1991. “RUSLE: Revised Universal Soil Loss Equation.” Journal of Soil and Water Conservation 46 (1): 30–33. https://www.jswconline.org/content/46/1/30.
Swarnkar, Somil, Anshu Malini, Shivam Tripathi, and Rajiv Sinha. 2018. “Assessment of Uncertainties in Soil Erosion and Sediment Yield Estimates at Ungauged Basins: An Application to the Garra River Basin, India.” Hydrology and Earth System Sciences 22 (4): 2471–85. https://doi.org/10.5194/hess-22-2471-2018.
Thapa, Pawan. 2020. “Spatial Estimation of Soil Erosion Using RUSLE Modeling: A Case Study of Dolakha District, Nepal.” Environmental Systems Research 9 (1): 15. https://doi.org/10.1186/s40068-020-00177-2.
Zanaga, Daniele, Ruben Van De Kerchove, Wanda De Keersmaecker, Niels Souverijns, Carsten Brockmann, Ralf Quast, Jan Wevers, et al. 2021. “ESA WorldCover 10 m 2020 V100.” Zenodo. https://doi.org/10.5281/ZENODO.5571936.